The following list describes some of the equations used in many stormwater engineers’ daily work. In some cases, an engineer may not directly apply these equations in a calculation/spreadsheet exercise. Rather, they may use these equations when preparing a hydraulic model. In such cases, it is still important to understand the theory/equations behind a hydraulic modeling program to ensure that the limitations and underlying assumptions are appropriate for the project.
1. Manning’s Equation
Manning’s equation is the most commonly used open channel flow equation. It is an empirical equation that is applicable to uniform flow conditions. Manning’s equation is used to calculate conveyance in HEC-RAS, which is a widely used hydraulic modeling program developed by the United States Army Corps of Engineers (USACE).
Manning’s equation was developed by Robert Manning, an Irish engineer, in 1894 as an alternative to Chezy’s equation (which is still used in some parts of the world). Ironically, Manning did not like his own equation because it is dimensionally incorrect and because it was difficult to calculate the cube root of a number in those days.
Manning’s equation is as follows:
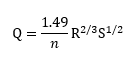
where,
Q is flow (cfs),
R is the hydraulic radius (flow area/wetted perimeter) (ft2/ft),
S is friction slope (ft/ft), and
n is Manning’s roughness value.
Under the assumption of uniform flow conditions, the channel slope is the same as the slope of the energy grade line. Therefore, it can be assumed that the friction slope (S) component of the equation is equal to the channel slope.
Although Manning’s n values are commonly referred to as the Manning’s roughness coefficient, Manning’s n values actually account for energy losses due to a variety of things such as friction losses, flow separation, turbulence, flow depth, and very sudden contractions or expansions. This means that Manning’s n value is not just based on channel roughness. It should also be noted that published n-values should not be used for materials other than water. To learn more about selecting an appropriate Manning’s n value check out this blog post:
2. Rational Method
The rational method/formula is used to determine a peak flow rate. Peak flow is a design parameter used to size storm drains and culverts. The rational method has been used widely in the United States since the early 1900s. It is worth noting that this formula should only be applied to drainage areas less than 1 square mile. The rational method also assumes that rainfall occurs at a constant rate, the runoff coefficient is constant, and rainfall is spatially uniform over the drainage area.
The rational method is as follows:
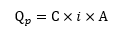
where,
Qp = peak flow rate (cfs),
C = runoff coefficient,
i = intensity (in/hr), and
A = drainage area (acres).
Intensity is based on time of concentration. After determining the time of concentration for your drainage area, you can use the NOAA Precipitation Data Frequency Server to determine the rainfall intensity for the design storm’s recurrence interval (e.g., 2-year, 10-year, 100-year, etc) and time of concentration. Because A is in acres, Qp is technically in ac-in/hr. However, Qp is reported as cfs because the conversion factor for converting ac-in/hr to cfs is 1.008.
The table below lists appropriate runoff coefficients for various land uses. A higher C value corresponds to more runoff. Thus, smaller areas with poorly draining soils should be assigned higher C values. In contrast, larger areas with well-draining soils should be assigned lower values.
| Land Use | C |
| Agricultural Land | 0.05 – 0.3 |
| Pasture | 0.05 – 0.3 |
| Unimproved/Vacant Land | 0.1 – 0.3 |
| Parks | 0.1 – 0.25 |
| Cemeteries | 0.1 – 0.25 |
| Railroad Yards | 0.2 – 0.35 |
| Playgrounds (except for asphalt or concrete) | 0.2 – 0.35 |
| Neighborhood Business District | 0.5 – 0.7 |
| City/Downtown Area | 0.7 – 0.95 |
| Single Family Residential | 0.3 – 0.5 |
| Multi-Family Residential (Detached) | 0.4 – 0.6 |
| Multi-Family Residential (Attached) | 0.6 – 0.75 |
| Apartments, Condominiums | 0.5 – 0.7 |
| Light Industrial | 0.5 – 0.8 |
| Heavy Industrial | 0.6 – 0.9 |
| Impervious Surface | 0.8 – 0.95 |
3. SCS Curve Number Method
The Soil Conservation Service (SCS) Curve Number Method is used to estimate runoff volume. The SCS method of estimating stormwater runoff from rainfall was the result of several field investigation efforts that took place in the 1940s and 1950s (Mockus, 1949; Sherman, 1942; Andrews, 1954; and Ogrosky, 1956). The passage of the Watershed Protection and Flood Prevention Act in August 1954 resulted in several small watershed studies associated with small watershed planning and served as a major catalyst for developing the SCS Curve Number Method. Originally, the SCS Curve Number method was developed to estimate runoff from agricultural watersheds. Today, the SCS Curve Number method is widely used in applied hydrology and to estimate urban runoff. However, more recent studies have demonstrated that some updates to the equations associated with the SCS curve number method may be necessary to accurately represent current conditions.
Runoff can be estimated using the SCS Curve Number Method by applying the equation below:
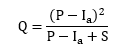
where,
Q is stormwater runoff depth (in),
P is rainfall (in),
S is potential maximum retention after runoff beings (in), and
Ia is initial abstraction (in).
Initial abstraction (Ia) includes all losses before runoff begins. Such losses include water intercepted vegetation, evaporation, and infiltration. Initial abstraction is correlated with the curve number (CN) and is presented as a percentage of the potential maximum retention after runoff begins (S) as shown in the equations below.
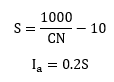
The initial abstraction ratio (Ia/S) has traditionally been assumed to be 0.2. However, recent studies have demonstrated that a value of 0.05 is more appropriate, especially in urban areas (Lim et al. 2006; Hawkins et al. 2002). The relationship between S0.2 and S0.05 is shown below. This relationship was developed by Hawkins et al. (2002) by performing a least squares regression.
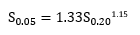
where,
S0.05 when Ia/S is 0.05 (in) and
S0.20 when Ia/S is 0.20 (in).
The revised SCS runoff equation is as follows:
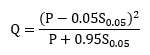
A runoff curve number (CN) is an empirical parameter based on land use and hydrologic soil group (HSG). A table of appropriate curve numbers can be found in Part 630, Chapter 10 of the United States Department of Agriculture (USDA) Natural Resources Conservation Service (NRCS) National Engineering Handbook (NEH).
4. Orifice Equation
Orifices are openings through which flow is conveyed by the difference in energy (head) between the upstream and downstream sides of the opening. Orifices are commonly used to regulate the flow from detention ponds and regulate the flow through sluice gates. The orifice equation can also be used to approximate the flow through a submerged culvert that is under inlet control.
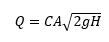
where,
Q is flow from an orifice (cfs),
C is the orifice coefficient,
g is the acceleration due to gravity (32.2 ft/s2), and
H is the elevation difference between the upstream water surface and the center of the orifice (ft).
In many cases, the orifice coefficient is assumed to be 0.6.
5. Weir Equation
A weir is a notch or gap over which water flows. The lowest point of the weir or the edge over which water flows is called the crest. The stream of water that flows over the weir is called the nappe. Weirs can be classified as sharp-crested or broad-crested. A sharp-crested weir has a sharp upstream edge which results in a nappe that flows clear of the crest. In contrast, a broad-crested weir has a crest that extends horizontally in the direction of flow far enough to support the nappe.
Weirs are often used as emergency spillways that are designed to convey flows from large storm events, regulate flow in channels, and measuring flow rates. In addition, flow over bridge decks or roadways can be approximated using the weir equation. The standard weir equation is as follows:
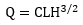
where,
Q is the flow over the weir (cfs),
C is the weir coefficient (ft1/2/s),
L is the length of the weir crest (ft), and
H is the head (water surface elevation – elevation of crest) over the weir crest (ft).
The weir coefficient accounts for head loss, energy losses due to contraction, and other energy loss variables. Unlike the orifice coefficient, the weir coefficient takes into account the constant 2g as shown in the equation below. Thus, weir coefficients differ depending on whether you are using English or SI units.
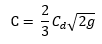
where,
Cd is the coefficient of discharge and
g is the acceleration due to gravity (ft/s2).
6. Energy Equation
The law of conservation of energy states that the total energy of any closed system (for which energy and matter transfer through the system boundary is not possible) is constant. Energy can be transformed from one form to another, but it can be neither created nor destroyed. The total energy in a system is the sum of potential energy, kinetic energy, and internal/molecular forms of energy. In hydraulic analyses/applications, the internal forms of energy are negligible and, thus, typically not considered.
In hydraulics, energy is often reported in units of energy per weight, which results in units of length. This way of expressing units of energy is referred to as “head.”
The energy equation is applied in many hydraulic modeling software programs. For example, in HEC-RAS, water surface profiles are generated based on the energy equation. The energy equation is as follows:
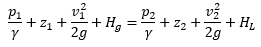
p1, p2 is pressure (lb/ft2),
γ is the specific weight of water (62.4 lb/ft3),
z1, z2 is the elevation above a defined datum,
v1, v2 is flow velocity (ft/s),
g is the acceleration due to gravity (ft/s2),
Hg is head gain from a pump (ft),
HL is head loss due to friction, contraction/expansion, or other energy losses (ft).
The hydraulic grade line is the sum of pressure head and elevation head. In open channel flow, the hydraulic grade is equal to the water surface elevation. The energy grade line is the sum of the hydraulic grade and the velocity head (v2/2g).
7. Average End Area Method
The average end area method is used to estimate earthwork volumes. The average end area method involves averaging two cross-sectional areas of earthwork and multiplying by the distance between two areas. It is worth noting that the average end area method often overestimates actual soil volume. However, as an approximation, it is accurate enough for most situations, especially for stormwater applications.
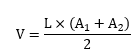
where,
L = length between end areas (ft),
A1, A2 = end area (ft2), and
V = earthwork volume (ft3).
Stationing is used to represent distances along an alignment. The number in front of the plus (+) sign represents hundreds of feet. Thus, you can omit the + sign and read the station like a normal number. For example, the distance between 1+50 and 1+00 is 50 feet (150-100).
8. Hazen-Williams Equation
The Hazen-Williams equation is used to calculate friction loss in pipes. For this reason, the Hazen-Williams equation is commonly used to design pressure pipes and conveyance piping for active rainwater harvesting systems. Like some of the other equations on this list, the Hazen-Williams equation is an empirical equation that should not be used for fluids other than water.
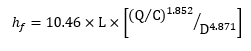
where,
hf is friction loss (ft),
L is equivalent pipe length (the physical pipe length + equivalent pipe length due to friction loss for pipe fittings and valves) (ft),
Q is flow (gpm),
C is the friction coefficient based on internal pipe roughness, and
D is inner pipe diameter (inches).
Understanding friction loss within a pipe allows the designer/engineer to select a pump that can convey water to where it needs to go.
9. Horton Infiltration Equation
A widely applied method of calculating the infiltration capacity of soil is the Horton infiltration equation (Horton, 1939). The Horton infiltration equation accounts for a decreasing rate of infiltration over time to account for the fact that the rate of infiltration decreases as soil becomes more saturated. This assumption is applicable for conditions in which the rainfall intensity is greater than the infiltration capacity.
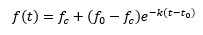
where,
f(t) is the infiltration rate (in/hr) at time t (min),
fc is the steady-state infiltration rate that occurs at a sufficiently long time after the storm begins,
f0 is the initial infiltration rate at the time that infiltration begins (t = t0), and
k is the decay coefficient (min-1).
The following table lists the values recommended by Rawls et al. (1976).
| Soil Type | f0 (in/hr) | fc (in/hr) | k (min-1) |
| Alphalpha Loamy Sand | 19.0 | 1.4 | 0.64 |
| Carnegie Sandy Loam | 14.8 | 1.8 | 0.33 |
| Dothan Loamy Sand | 3.5 | 2.6 | 0.02 |
| Fuquay Pebbly Loamy Sand | 6.2 | 2.4 | 0.08 |
| Leefield Loamy Sand | 11.3 | 1.7 | 0.13 |
| Tooup Sand | 23.0 | 1.8 | 0.55 |
10. Time of Concentration
The time of concentration (tc) is the amount of time it takes for a drop of water to travel from the point that is furthest away (hydraulically) from the outlet of a watershed to the outlet of the watershed. For small drainage areas, such as a parking lot, the time of concentration is assumed to be 5 minutes.
The most most common way to calculate time of cocentration (at least in the United States) is to apply methodology outlined in Natural Resources Conservation Service (NRCS) Technical Release 55 (TR-55). The following paragraphs will briefly describe the way time of concentration is computed in TR-55.
To estimate time of concentration, begin by drawing the longest flow path for your drainage area. Then separate the flow path into three lengths: sheet flow (< 300 feet), shallow concentrated flow, and concentrated flow (channel/ditch flow).
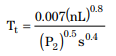
where,
Tt is travel time for sheet flow (hr),
n is the Manning’s roughness coefficient for sheet flow (see table provided in TR-55),
Lo is the length of sheet flow (ft),
P2 is the 2-year, 24-hour rainfall depth (inches), and
S is the slope of hydraulic grade line (typically approximated as land slope) (ft/ft).
The travel time for shallow concentrated flow and concentrated flow are calculated using the same equation.
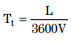
where,
Tt is travel time for sheet flow (hr),
L is flow length (ft), and
V is velocity (ft/s).
The velocity for shallow concentrated flow can be determined using a nomograph that is provided on page 3-2 of TR-55. The velocity for concentrated flow can be calculated using Manning’s equation.
Finally, add up the travel time for all of the segments along the watershed’s flow path to determine the time of concentration. If applicable, remember to convert from hours to minutes.