The Manning’s roughness coefficient, which is also commonly referred to as Manning’s n, is an empirical parameter that represents energy loss due to a variety of things such as friction losses, flow separation, turbulence, and very sudden contractions or expansions. Manning’s n values are applied to Manning’s equation, which calculates open channel flow.
In HEC-RAS, Manning’s n values are used to perform water surface profile computations. This means that Manning’s roughness coefficient is one of the most important parameters in hydrologic and hydraulic modeling. Selecting Manning’s n values that are appropriate for your hydraulic model is both a science and an art. While there are guidelines available for selecting Manning’s roughness coefficients, there is no hard and fast rule for determining the “best” Manning’s n value for a specific situation. Many water resources engineers will tell you that selecting appropriate Manning’s n values comes with experience.
There are a variety of factors that affect channel roughness including the following:
- Stream bed material and grain size,
- Surface irregularities within the channel bed,
- Channel bedforms (e.g., ripples, dunes, transition, and plane bed),
- Erosion and depositional characteristics,
- Meandering tendencies,
- Channel obstructions (e.g., overtopped trees, root wads, beaver dams, debris),
- Depth of water,
- Change in channel geometry,
- Vegetation along the banks and within the channel, and
- Other abrupt changes in energy and/or momentum.
It can be difficult to capture everything in the list above into a single value. When selecting Manning’s n values (or any parameter for a hydraulic model) for your HEC-RAS model, it is important to report your rationale and back up your assumptions with scientific journals and guidance documents. The following blog post will discuss how to apply appropriate Manning’s roughness coefficients to one-dimensional (1D). It should be noted that this blog post will not contain tables listing Manning’s n values. Rather, it will be a discussion of the methods used to determine an appropriate Manning’s n value for your hydraulic model.
Manning’s n for 1D HEC-RAS Models
When preparing a 1D hydraulic model with HEC-RAS, Manning’s n values are most commonly applied to the left overbank, channel, and right overbank. However, HEC-RAS allows the user to add Manning’s n values in such a way that more fully represents what is in the field. Some of these features (e.g., horizontal variation, vertical variation, and seasonal roughness coefficients) will be discussed in subsequent sections.
As previously mentioned, Manning’s roughness coefficients could be explained as a sort of “uncertainty” coefficient where we account for losses in energy throughout a channel profile. For example, in a 1D hydraulic model, Manning’s roughness parameter can account for:
- friction losses associated with the bed material in the channel and floodplain,
- drag losses associated with vegetation or obstructions in the channel or floodplain,
- form losses due to turbulence in the channel or floodplain,
- changes in cross-section geometry,
- bend losses in the channel, and
- other losses/uncertainty that we can also lump into Manning’s n.
This means that Manning’s n values do not just represent the “roughness” of the stream bed. As such, it is important that modelers consider more than just surface roughness when selecting a set of Manning’s roughness coefficients for a hydraulic model. For example, when modeling drop structures along a stream, Manning’s n values are often increased inside of a stilling basin to account for the significant energy loss associated with a hydraulic jump.
How to choose an appropriate Manning’s n (1D)
The most common source of Manning’s n values is those listed in Chow (1959). The tables presented in Chow (1959) list minimum, normal, and maximum values for a variety of common channel types and closed conduits flowing partially full. For very wide streams, vegetation and geometry change have a lesser effect on the Manning’s roughness, and channel bed material may be more important when selecting a Manning’s n value. Some of the resources I use to select Manning’s n values for 1D HEC-RAS models include:
- Chow’s Open Channel Hydraulics book (Chow, 1959)
- An excerpt of the Manning’s n values presented in Chow (1959) is available in Chapter 3 of the HEC-RAS Hydraulic Reference Manual
- Chapter 5 of United States Army Corps of Engineers (USACE’s) Hydraulic Design of Flood Control
- Some agencies will specify the Manning’s n value for certain models. For example, the Los Angeles County Sedimentation Manual specifies that a Manning’s n value of 0.025 should be applied to hydraulic models prepared for the purpose of estimating scour depths.
- Engineers who regularly work on open channel hydraulic projects will eventually develop an intuition for appropriate Manning’s n values, especially if their projects are within the same general geographic area. While one should never rely on engineering judgment alone, this experience is valuable when evaluating different techniques for adopting Manning’s n values.
- The United States Geological Survey’s Roughness Characteristics of Natural Channels.
- County-specific hydraulic design manuals. Some local jurisdictions list Manning’s n values they will accept in their published hydrologic or hydraulic design manuals. These manuals are typically available online.
- Cowan’s equation is a formula used to derive an analytic estimate of Manning’s n values and is described in (Cowan, 1956).
Manning’s roughness coefficient varies along the channel cross-section and decreases as water depths increase. The following section will discuss how to address these variations in HEC-RAS.
Horizontal variation in Manning’s n values (1D)
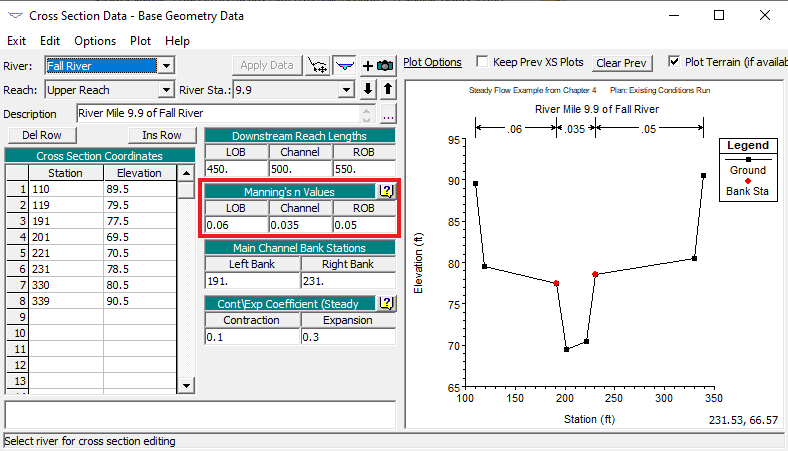
In a 1D HEC-RAS model, Manning’s n values are typically entered for the left overbank, channel, and right overbank at every cross-section. The image below illustrated how data is entered in this fashion within HEC-RAS.
However, it is possible to enter Manning’s n values to account for changes in roughness along a cross-section. For example, a cross-section may have a grassy floodplain, concrete sloped banks, and a sediment channel bottom. These changes in surface roughness should be accounted for when developing an HEC-RAS model that will be used for the purpose of delineating floodplains. To enter Manning’s n values in a way that represents such a situation, click Options at the top of the Cross Section Data Editor. Then select Horizontal variation in n values. The image below shows an example of a cross-section that has Manning’s n values entered using the horizontal variation feature.
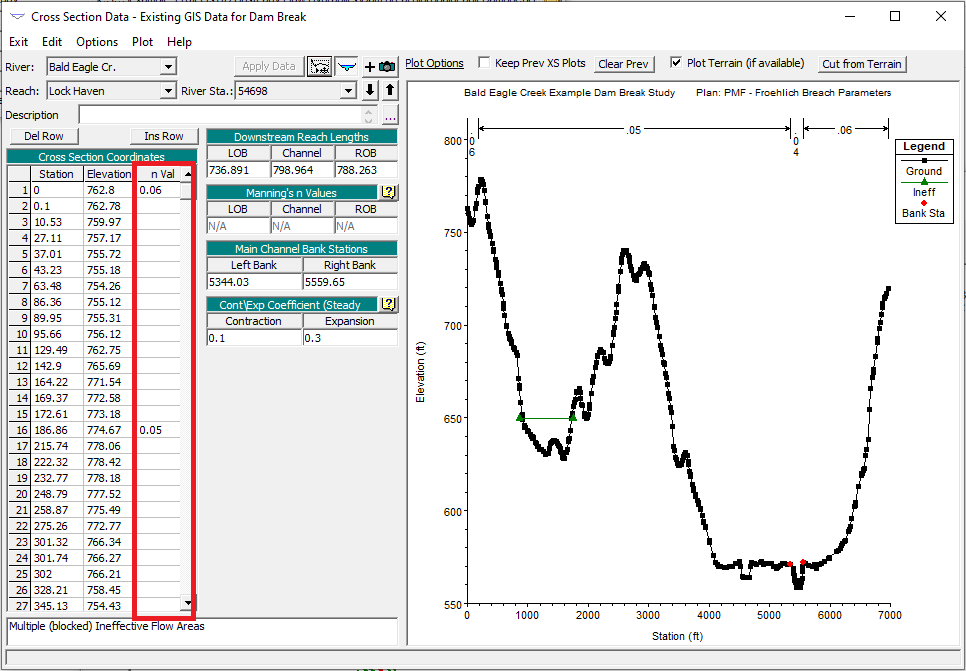
It is important to note that Manning’s n values can get messy if you interpolate between cross-sections that contain horizontal variation in Manning’s roughness coefficients.
Vertical variation in Manning’s n values (1D)
Manning’s roughness values vary depending on the depth of water. Manning’s roughness increases as water depths become shallower. At very shallow depths, Mannings n values can be as high as 0.2 (even higher in some cases).
Users can account for the variation of Manning’s n based on depth in HEC-RAS. This is not a commonly used feature, but it can be useful for calibration and model stabilization purposes. To use the vertical variation feature in HEC-RAS, click Options at the top of the Cross Section Data Editor. Then select Vertical variation in n values. The following box will appear.
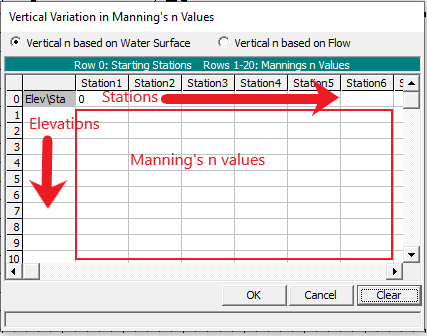
Alternatively, you can vary Manning’s n value by flow rate. However, this is only applicable to unsteady flow models.
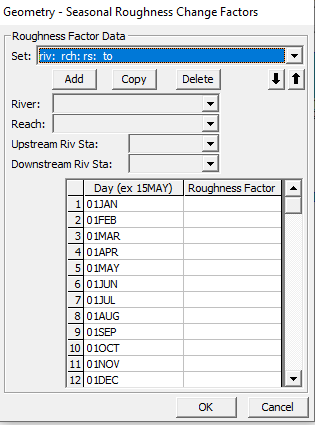
Seasonal Roughness Factors
Finally, HEC-RAS users can also enter seasonal roughness factors that account for the variation in Manning’s n with season, which is useful for long simulations. Manning’s roughness may change with season due to cycles in vegetation growth and ground cover. To a lesser extent, Manning’s n values may also be seasonal due to water viscosity with temperature. To apply season roughness factors, click Tools in the Geometry Data Editor and select Seasonal Roughness Factors. It is important to note that you are applying factors that will be multiplied by the Manning’s n values entered into the cross section data editor rather than actual Manning’s roughness coefficients.