I have heard the term “attenuation” thrown around throughout my career. However, it took me a long time to actually understand what the term means. It turns out that flow attenuation is actually a fairly simple concept. In summary, attenuation of flow refers to any means by which peak flow is reduced. Therefore, the attenuation of flow is the difference between the peak of the inflow hydrograph and the outflow hydrograph.
Flow attenuation is calculated by subtracting the outflow/downstream peak discharge from the upstream/inflow peak discharge. The flow attenuation divided by the upstream/inflow peak flow rate is the percent attenuation for a given event. The time difference between the peak of the inflow hydrograph and the outflow hydrograph is called lag.
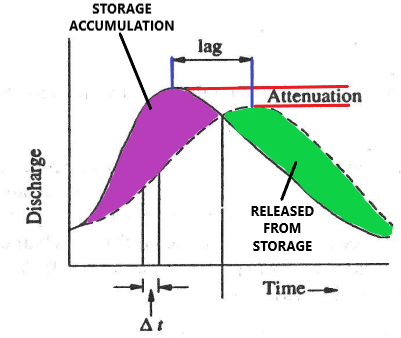
Flow Attenuation in Hydraulic Modeling
An unsteady flow model should be used to model situations (e.g., wide floodplains) where there is significant flow attenuation. When a channel has a wide floodplain, it can take a significant amount of time to fill the floodplain with water. While the floodplain is filling, less flow is being conveyed downstream. Unlike a steady flow model, an unsteady flow model can adjust the hydrograph based on whether the volume in the flood wave is less than or greater than the amount of storage available in the channel.
Factors That Affect Attenuation
- Manning’s n values – increasing Manning’s n values will increase attenuation.
- Ineffective flow areas – ensuring that all ineffective flow areas are included in your cross sections will minimize the chance of underestimating flow attenuation.
- Storage Areas for offline storage.
- Bridge, culvert, weir coefficients.
Flow Attenuation Parameter
One way to help determine whether the flow attenuation in your study reach warrants preparing an unsteady flow model rather than a steady flow model is to calculate the attenuation parameter (Samuels and Gray, 1982). If γ is less than 6×10-7 (for US units), steady flow modeling can be used to represent attenuation with as much accuracy as an unsteady model.
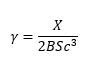
where,
γ is the attenuation parameter (ft),
X is the curvature of the peak of the flood hydrograph,
B is the mean surface width (ft),
S is the mean bed slope of the channel reach (ft/ft), and
c is the mean propagation speed of the flood peak (ft/s).
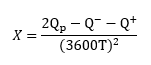
where,
Qp = peak flow (cfs)
Q– is flow T hours before the peak (cfs)
Q+ is flow T hours after the peak (cfs)
T is typically chosen to encompass 2/3 of the hydrograph.
The mean propagation speed of the flood peak is calculated using the following equation.
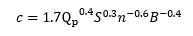
where,
n = Manning’s n